Applications
 Part of the Oxford Instruments Group
Part of the Oxford Instruments Group
Expand
Collapse
20th January 2021 | Author: Dr Pat Trimby
My life as Oxford Instruments’ EBSD Product Manager would be much easier if EBSD was a simpler technique. The fact that it involves diffraction and crystallography is enough to put many people off, even before they encounter the complexities of pole figures or orientation distribution functions. However, the improvements made to both EBSD software and hardware over the past few decades have significantly broadened the technique’s appeal. This is a sign of real progress, but the technique is still challenging to newcomers in many ways. Leaving aside the demands on sample preparation, geometry, and the complexities of how to process EBSD data; I would like to focus on one of the most frequent topics that new users ask:
In 2 previous blogs, I have already discussed ways to optimise the set-up of your CMOS EBSD detector: this included advice on which detector mode to use and also how to set a suitable camera exposure time. Here I am going to assume that you have overcome the challenges of sample preparation, that you have set up your sample in the SEM and that you are able to get good diffraction patterns using a suitable detector mode. The decisions to be made now involve the selection of the best parameters for turning the diffraction patterns into reliable, high quality orientation data.
Firstly, I need to outline the basic principles of our indexing algorithm. This was completely overhauled in an early version of AZtec (v. 2.0) with the introduction of the Tru-I indexing method and has been progressively optimised in subsequent releases. Tru-I works with groups of 4 bands (so-called “quadruplets”) and indexes each quadruplet down to a reflector group level (e.g. type {111}, {200} etc.), before determining the most likely solution (at an individual reflector level) via an accumulator matrix. The final step will be to convert that solution into the necessary 3D orientation relative to the sample surface.
The reason to use quadruplets, rather than triplets for example, comes down to basic maths: for a given number of detected Kikuchi bands, there are many more possible groups of 4 bands than there are groups of 3 bands (for example, with 10 detected bands there are 210 possible quadruplets compared to 120 possible triplets). This results in a higher degree of reliability in the indexing process – you can be more confident in your data and will have less indexing noise and fewer incorrect solutions during your analysis.
There are of course further complexities to our indexing algorithm that are beyond the scope of this blog, but this brief overview is useful in helping us to understand some of the recommended settings. I will focus on the band detection and indexing settings, as these are critical for routinely getting reliable results. More advanced users will often want to tweak these settings in order to optimise the results on more complex samples, but these guidelines will help to deliver great results on the majority of sample types.
The main message for setting up band detection is very simple:
The answer relates to the developments that have been implemented in the TKD optimised mode. TKD patterns often contain very broad Kikuchi bands, due to the increased distortion resulting from the technique’s unusual geometry, and these broad bands can cause problems for the standard EBSD band detection process. In response to this, our TKD optimised band detection mode involves an additional peak search process within the Hough space that is performed at a higher Hough resolution, resulting in a much higher accuracy of Kikuchi band edge detection.
This also has the same benefits for conventional EBSD pattern analysis – the improved band edge detection will result in more reliable data, and a better angular precision that is not dependent on the user-specified resolution of the Hough transform. This can be seen in the following graph, showing the angular precision (measured using kernel average misorientation – KAM – values from analyses of a Si single crystal) for different band detection settings and Hough resolutions.
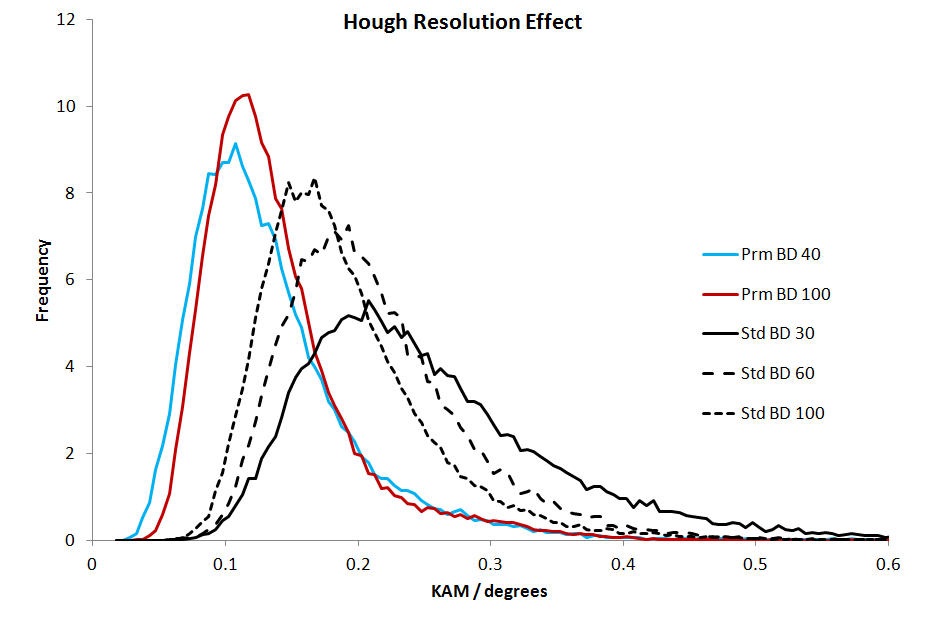
The TKD-optimised band detection, here referred to as “Primary band detection” (Prm BD), shows significantly better angular precision than the standard EBSD-optimised band detection (Std BD). What is also noticeable is that the angular precision of the standard band detection is closely linked to the user-defined Hough resolution – a Hough resolution of 100 results in significantly better precision than a Hough resolution of 60, for example. However, for the TKD optimised band detection, there is essentially no difference between the curves when using a Hough resolution of 40 or 100.
As seen in the above graph, if you use the TKD-optimised band detection then the choice of Hough resolution is far less critical. I would advise using the default value of 60, lowering it to 40 if you need to push the system to work with the fastest detector speeds (for example, if you wish to map at >4000 patterns per second with our Symmetry S2 detector).
In cases where very high angular precision is important, it makes sense to use our Refined Accuracy band detection method. This is an iterative approach that performs the same initial indexing step using the TKD-optimised band detection, but then refines the solution by fitting the curved Kikuchi band edges in the simulation to their corresponding positions in the EBSP itself. This works best with higher resolution EBSPs (for example, Speed 1 or Resolution modes with our Symmetry detector range), although it will also limit the maximum speed of analysis. However, if you want to look at the details of deformation, view dislocation arrays, or characterise low angle boundaries effectively: Refined Accuracy is the perfect tool and can give a precision close to 0.01° in some cases. For more information I would advise watching our Tips and Tricks video “Acquiring EBSD Data with High Angular Precision”.
I love some of the images of deformed grains that can be generated from Refined Accuracy data, including the dataset featured in the video above. Here Refined Accuracy has revealed the complex dislocation wall structures within a single deformed Ni grain; my only problem is that I cannot decide whether I prefer the KAM map or the grain relative orientation deviation (GROD) map!
I’m hopeful that these suggestions will help you to collect even better data with your AZtecHKL EBSD systems. Although we cannot completely remove the complexities of the EBSD technique, we are planning some significant improvements to our AZtecHKL EBSD software to continue to improve usability and accessibility.
As ever, keep an eye on our website and don’t hesitate to contact your local Oxford Instruments support team if you want expert advice on using any of our nanoanalysis products.
We send out monthly newsletters keeping you up to date with our latest developments such as webinars, new application notes and product updates.